 International
Newsletter on Physics Education
International
Newsletter on Physics Education


International Commission on Physics Education
International Union of Pure and Applied Physics
Number 33
November 1996
| Table of Contents |
The 27th International Physics Olympiad
in Oslo, Norway, 1996
Arnt Inge Vistnes, Organizing Committee Director
The interest in physics and natural sciences in general may be declining in elementary school and high school, but when it comes to the best students we see at an international physics olympiad, the level is still outstanding. The problems we presented to the 260 students from 55 countries in Oslo this year were difficult, but even so, the best students got 47.5 points out of 50 possible. However, there is a huge difference between the best and the not-so-good students, even if only five students are allowed from each country. This might indicate differences in the quality and quantity of teaching in the various countries, but of course it might also be related to the kind of special training some students receive during the time between they are elected as participants in the physics olympiad and the olympiad itself.
The program during the olympiad was as follows:
During the Closing Ceremony, 1974 Nobel Laureate in Physics Dr. Ivar Giaever, awarded the 20 best students with their gold medals. Best were Yurun Liu from China, Rui Zhang from China (one of the few girls in this competition), Arend Bayer from Germany, Kaiwen Xu from China, and 13 year-old Chris Hirata from USA. Results and ranking of nations are available on our web pages (http://anyon.uio.no/ipho/).
At the meetings in the International Board, one question had a lot of interest: should there be written in the statutes that organizers could ask for a "voluntary fee" from the various participating nations or not? Norway was allowed to ask for such a fee (decided in Canberra in 1995), and without this fee (US$ 300 per person), the funding of this olympiad would have been a disaster. It is not so easy to get sponsors from industry to such an event in a country like Norway, and the Ministry of Education contributed with about 25% of the total costs. I am afraid that the decision made by the International Board, not to put anything regarding a "voluntary fee" into the statutes, will hamper the Physics Olympiad movement in the future.
The Physics Olympiads is certainly a great stimulation
for the students. On the other hand, as Professor Eivind Osnes, head of
the Department of Physics at the University of Oslo, expressed during the
final dinner, it is more questionable how great an inspiration a physics
olympiad is for teaching physics. Should one use more time during these
olympiads to discuss teaching experiences in the different countries among
the leaders?
| In scientific thought we adopt the simplest theory which will explain
all the facts under consideration and enable us to predict new facts of
the same kind. The catch in this criterion lies in the word 'simplest'.
It is really an aesthestic canon such as we find implicit in our criticisms
of poetry or painting. The layman finds such a law as
dx/dt = K d2x/dy2 much less simple than 'it oozes', of which it is the mathematical statement. The physicist reverses this judment, and his statement is certainly the more fruitful of the two, so far as prediction is concerned. It is, however, a statement about something very unfamiliar to the plain man, namely, the rate of change of a rate of change. -J.B.S. Haldane in "Science and theology as art forms", Possible Worlds, (Chatto & Windus, London, 1927) |
Problem 1 (the 5 parts of this problem are unrelated)
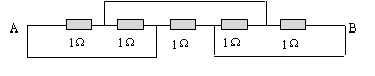
Determine the resulting resistance R between A and B.
(1 point)
c) A thermally insulated piece of metal is heated under atmospheric pressure by an electric current so that it receives electric energy at a constant power P. This leads to an increase of the absolute temperature T of the metal with time t as follows:
T(t) = T0 [1+a(t-t0)]1/4
Here a, t0 and T0 are constants. Determine the heat capacity Cp(T) of the metal (temperature dependent in the temperature range of the experiment). (2 points)
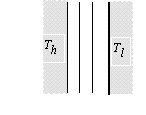
d) A black plane surface at a constant high temperature Th is parallel to another black plane surface at a constant lower temperature Tl. Between the plates is vacuum.
In order to reduce the heat flow due to radiation, a heat shield consisting of two thin black plates, thermally isolated from each other, is placed between the warm and the cold surfaces and parallel to these. After some time, stationary conditions are obtained.
By what factor x is the stationary
heat flow reduced due to the presence of the heat shield? Neglect end effects
due to the finite size of the surfaces. (1.5 points)
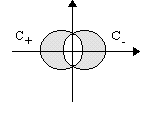
e) Two straight and very long nonmagnetic conductors C+ and C-, insulated from each other, carry a current I in the positive and the negative z direction, respectively. The cross sections of the conductors (shaded in the figure) are limited by circles of diameter D in the x-y plane, with a distance D/2 between the centers. Thereby the resulting cross sections each have an area (p/12 +Ö3/8 )D2. The current in each conductor is uniformly distributed over the cross section.
Determine the magnetic field B(x,y) in the
space between the conductors. (4 Points)
Problem 2
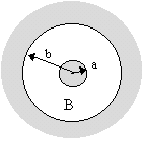
The space between a pair of coaxial cylindrical conductors is evacuated. The radius of the inner cylinder is a, and the inner radius of the outer cylinder is b, as shown in the figure below. The outer cylinder, called the anode, may be given a positive potential V relative to the inner cylinder. A static homogeneous magnetic field B parallel to the cylinder axis, directed out of the plane of the figure, is also present.
We study the dynamics of electrons with rest mass m and charge -e. The electrons are released at the surface of the inner cylinder. Induced charges in the conductors are to be neglected.
a) First potential V is turn on, but B=0. An electron is set free with negligible velocity at the surface of the inner cylinder. Determine its speed v when it hits the anode, Give the answer both when a non-relativistic treatment is sufficient, and when it is not. (1 point)
For the remaining parts of this problem a non-relativistic treatment suffices.
b) Now V=0, but the homogeneous magnetic field B is present. An electron starts out with an initial velocity v0 in the radial direction. For magnetic fields larger than a critical value Bc, the electron will not reach the anode. Make a sketch of the trajectory of the electron when B is slightly more than Bc. Determine Bc. (2 points)
From now on both the potential V and the homogeneous magnetic field B are present.
c) The magnetic field will give the electron a non-zero angular momentum L with respect to the cylinder axis. Write down an equation for the rate of change dL dt of the angular momentum. Show that this equation implies that
L - keBr2
is constant during the motion, where k is a definite pure number. Here r is the distance from the cylinder axis. Determine the value of k. (3 points)
d) Consider an electron, released from the inner cylinder with negligible velocity, that does not reach the anode, but has a maximal distance from the cylinder axis equal to rm. Determine the speed v at the point where the radial distance is maximal, in terms of rm.
e) We are interested in using the magnetic field to regulate the electron current to the anode. For B larger than a critical magnetic field Bc, an electron, released with negligible velocity, will not reach the anode. Determine Bc. (1 point)
f) If the electrons are set free by heating the inner
cylinder an electron will in general have an initial non-zero velocity
at the surface of the inner cylinder. The component of the initial velocity
parallel to B is vB, the components perpendicular to B
are vt (in the radial direction) and vj
(in the azimuthal direction, i.e. perpendicular to the radial direction).
Determine for this situation the critical magnetic field Bc for
reaching the anode. (2 points)
Problem 3
In this problem we consider some gross features of the
magnitude of mid-ocean tides on earth. We simplify the problem by making
the following assumptions:
(1) The earth and the moon are considered to be an isolated system,
(2) the distance between the moon and earth is assumed to be constant,
(3) the earth is assumed to be completely covered by an ocean,
(4) the dynamic effects of the rotation of the earth around its axis are neglected, and
(5) the gravitational attraction of the earth can be determined
as if all mass were concentrated at the center of the earth.
The following data are given:
Mass of the earth: M = 5.98x1024 kg
Mass of the moon: Mm = 7.3x1022 kg
Radius of the earth: R = 6.37x106 m
Distance between center of the earth and center of the moon: L =
3.84x108 m
The gravitational constant: G = 6.67x10-11 m3 kg-1 s-2
a) The moon and the earth rotate with angular velocity w about their common center of mass, C. How far is C from the center of the earth? (Denote this distance by l.)
Determine the numerical value of w. (2 points).

We now use a frame of reference that is co-rotating with the moon and the center of the earth around C. In this frame of reference the shape of the liquid surface of the earth is static.
In the plane P through C and perpendicular to the axis of rotation, the position of a point mass on the liquid surface of the earth can be described by polar coordinates r, j as shown in the figure. Here r is the distance from the center of the earth.
We will study the shape r(j) = R + h(j) of the liquid surface of the earth in the plane P.
b) Consider a point mass (mass m) on the liquid surface of the earth (in plane P). In our frame of reference it is acted upon by a centrifugal force and by gravitational forces from the moon and the earth. Write down an expression for the potential energy corresponding to these three forces.
Note: Any force F(r), radially directed with respect to some origin, is the negative derivative of a spherically symmetric energy V(r): F(r) = - V(r). (3 points)
c) Find, in terms of the given quantities M, Mm, etc, the approximate form h(j) of the tidal bulge.
What is the difference in meters between high tide and low tide in this model?
You may use the approximate expression
valid for a much less than unity.
In this analysis make simplifying approximations wherever
they are reasonable. (5 points)
Summary
The set of problems will cover a number of topics in physics.
In sections 1 and 2, some mechanical properties of a physical pendulum
will be explored and you should be able to determine the acceleration of
gravity. In section 3, a question in optics in relation to the experimental
setup will be asked. Then magnetic forces are added to the pendulum. In
section 4, the magnetic field from a large permanent magnet is measured
using an electronic sensor. Then in section 5 the magnetic moment of a
small permanent magnet will be determined.
Equipment
The following equipment is available (see Figure 1):
A. Large aluminum stand.
B. Threaded brass rod with a small magnet on one end, painted white, and
a tiny piece of iron on the other end.
C. Two nuts with a reflecting surface on one side.
D. Oscillation period timer (clock) with digital display.
E. Magnetic field (Hall) probe, attached to the large stand.
F. 9 V battery.
G. Multimeter, Fluke model 75.
H. Two leads.
I. Battery connector.
J. Cylindrical stand made of PVC (plastic material).
K. Threaded rod with a piece of PVC and a permanent magnet on the top.
L. Small PVC cylinder of length 25.0 mm (to be used as spacer).
M. Ruler.
The pendulum should be mounted as illustrated in Figure 1. The long threaded rod serves as a physical pendulum, hanging on the large stand by one of the nuts. The groove in the nut should rest on the two vertical blades on the large stand, thus forming the axis of rotation. The reflecting side of the nut is used in the oscillation period measurement, and should always face toward the timer.
The timer displays the period of the pendulum in seconds with a certainty of ±1 ms. The timer has a small infrared light source on the right-hand side of the display (when viewed from the front), and an infrared detector mounted close to the emitter. Infrared light from the emitter is reflected by the mirror side of the nut. The decimal point lights up when the reflected light hits the detector. For proper detection the timer can be adjusted vertically by a screw (see N in Figure 1). Depending on the adjustment, the decimal point will blink either once or twice each oscillation period. When it blinks twice, the display shows the period of oscillation, T. When it blinks once, the displayed number is 2T. Another red dot appearing after the last digit indicates low battery. If the battery needs to be replaced, ask for assistance.
The multimeter should be used as follows: Use the "VW" and the "COM" inputs. Turn the switch to the DC voltage setting. The display then shows the DC voltage in volts.
Figure 1: The equipment used.
The Physical Pendulum
A physical pendulum is an extended physical object of
arbitrary shape that can rotate about a fixed axis. For a physical pendulum
of mass M oscillating about a horizontal axis a distance l
from the center of mass the period T for a small angle oscillation
is:
Here g is the acceleration of gravity, and I is the moment of inertia of the pendulum about an axis parallel to the rotation axis but through the center of mass of the pendulum.
Figure 2 shows a schematic drawing of the physical pendulum you will be using. The pendulum consists of a cylindrical metal rod, actually a long screw, having length L, average radius R and at least one nut. The values of various dimensions and masses are summarized in Table 1. By turning the nut you can place it at any position along the rod. Figure 2 defines two distances, x and l, that describe the position of the rotation axis relative to the end of the rod and the center of mass of the pendulum, respecively.
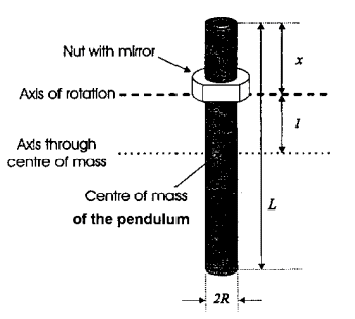
Figure 2: Schematic drawing of the pendulum with definition
of important quantities.
Section 1: Period of oscillation versus rotation axis position (4 marks)
a) Measure the oscillation period, T, as a function of the position x, and present the results in a table.
b) Plot T as a function of x in a graph. Let 1mm in the graph correspond to 1mm in x and 1ms in T. How many positions give an oscillation period equal to T = 950 ms, T = 1000 ms, and T = 1100 ms, respectively?
c) Determine the x and l values that correspond
to the minimum values in T.
Table 1: Dimensions and weights of the pendulum
Section 2: Determination of g (5 marks)
Consider a physical pendulum with a fixed moment
of inertia, I. The same period, T, may in some cases be obtained
for two different positions of the rotation axis. Let the corresponding
distances between the rotation axis and the center of mass be l1
and l2. Then the following equation is valid:
a) Figure 6 illustrates a physical pendulum with a axis of rotation displaced a distance l1 from the center of mass. Use the information given in the figure caption to indicate all positions where a rotation axis parallel to the drawn axis can be placed without changing the oscillation period.
b) Obtain the local value for the acceleration of gravity g as accurately as possible. Hint: there is more than one way of doing this. New measurements may be needed. Indicate clearly by equations, drawings, calculations etc. the method you used.
c) Estimate the uncertainty of your measurements and give
the value of g with error margins.
Section 3: Geometry of the optical timer (3 marks)
a) Use direct observation and reasoning to characterize, qualitatively as well as quantitatively, the shape of the reflecting surface of the nut (the mirror). (You may use the light from the desk lamp.)
Options (several may apply):
1. Plane mirror
2. Spherical mirror
3. Cylindrical mirror
4. Concave mirror
5. Convex mirror
In case of 2-5, determine the radius of curvature.
b) Consider the emitter in the timer to be a point source,
and the detector to be a simple photoelectric device. Make an illustration
of how the light from the emitter is reflected by the mirror on the nut
in the experimental setup (side view & top view). Figure 7 shows a
vertical plane through the timer display (front view). Indicate in this
figure the whole region where the reflected light hits this plane when
the pendulum is vertical.
Section 4: Measurement of magnetic field (4 marks)
You will now use an electronic sensor (Hall-effect sensor) to measure magnetic field. The device gives a voltage which depends linearly on the vertical field through the sensor. The field-voltage coefficient is
DV / DB = 22.6 V/T (Volt/Tesla).
As a consequence of its design the sensor gives a non-zero voltage (zero-offset voltage) in zero magnetic field. Neglect the earth's magnetic field.
Figure 3: Schematic of the magnetic field detector
system
a) Connect the sensor to the battery and voltmeter as shown above. Measure the zero-offset voltage, V0.
A permanent magnet shaped as a circular disk is mounted on a separate stand. The permanent magnet can be displaced vertically by rotating the mount screw, which is threaded identically to the pendulum rod. The dimensions of the permanent magnet are:
thickness t = 2.7 mm
radius r = 12.5 mm
b) Use the Hall sensor to measure the vertical magnetic field, B, due to the permanent magnet, along the axis of the cylinder (see Figure 4). Let the measurements cover the distance from y = 26 mm (use the spacer) to
y = 3.5 mm, where y = 1 mm corresponds to the sensor and permanent magnet being in direct contact. Plot a graph of your data for B versus y.
Figure 4: Definition of the distance y between the
top of the magnet and the active part of the sensor.
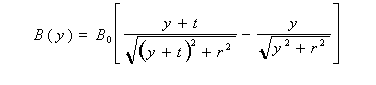
where t is the cylinder thickness and r is the radius.
The parameter B0 characterizes the strength of the magnet. Find
the value of B0 for your permanent magnet. Base your determination
on two measured B-values obtained at different y.
Section 5: Determination of magnetic dipole moment (4 marks)
A small magnet has been attached to the white end of the pendulum rod. Mount the pendulum on the stand with its magnetic end down and with x=100 mm (see figure 2). Place the large permanent magnet mount under the pendulum so that both the permanent magnet and the pendulum have a common axis. The alignment should be done with the permanent magnet in its lowest position in the mount. (Always avoid close contact between the permanent magnet and the magnetic end of the pendulum.)
a) Let z denote the air gap spacing between the permanent magnet and the lower end of the pendulum. Measure the oscillation period, T, as a function of the distance z. the measurement series should cover the interval from z=25 mm to z=5.5 mm. Use as small an oscillation amplitude as possible. Be aware of the possibility that the period timer might display 2T (see remark regarding the timer under Equipment). Plot T versus z.
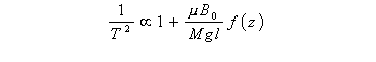
Here µ means "proportional to", m is the magnetic dipole moment of the small magnet attached to the pendulum and B0 is the parameter determined in section 4c. The function f(z) includes the variation in magnetic field with distance. In figure 5, the particular f(z) for our experiment is presented as a graph.
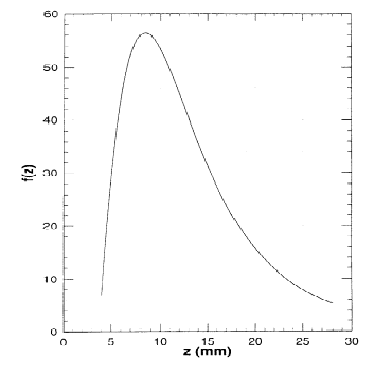
Select an appropriate point on the graph to determine the unknown magnetic moment m.
Figure 5. Graph of the dimensionless function f(z)
used in section 5b.
Figure 6. For use in section 2a. mark all
positions where a rotation axis (perpendicular to the plane of the paper)
can be placed without changing the oscillation period. Assume for this
pendulum (drawn on scale 1:1) that I/M = 2100x10-6 m2.
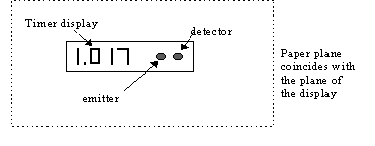
Figure 7. For use in section 3b. Indicate the
whole area where the reflected light hits when the pendulum is vertical.
| The easiest method of acquiring the scientific habit
is through acquiring the ability to express oneself clearly in discussing
and disputing scientific problems. This is what clarifies their import
and makes them understandable.
Ibn Khaldun (1332-1406) in The Muqaddimah. An Introduction to History |
The First European Project in Science Education: Research on Computer-Based Approaches to Labwork in Europe
Marie-Genevieve Séré, Université Paris, France
In 1995, the European Community launched a proposal in human and social sciences, including education. Numerous research teams took the opportunity to develop collaborations for common projects. Five percent of them have been granted, with only one in science education. This project has France as a coordinator, with Germany, Great Britain, Greece, Italy, and Denmark; 38 members altogether.
In this project, the main theme is the role of experiment in science teaching. The seven collaborative groups are working to the following general objectives:
· conceptualizing the place of labwork in science education by identifying the aptitudes that it can promote among students;
· producing illustrative material for particular approaches to labwork to promote specific aptitudes;
· elaborating a grid of criteria around which the effectiveness of labwork can be evaluated drawing on these aptitudes.
These objectives are addressed at the level of secondary school and the beginning of undergraduate programs at university for labwork in physics, chemistry and biology.
Consequently, the main activities are :
· comparative studies of existing approaches of labwork in the six countries involved. A descriptive tool has been developed which allows one to take into account the different dimensions of experiment-based teaching;
· surveys about teachers' and students' images of science (methods, results, processes, etc.) influencing the design of labwork, tasks and activities;
· two sets of case studies
to elicit students' processes of learning during different types of labwork,
and to study implementation of new technologies for modeling, simulation,
data gathering and processing.
Finally, this research will contribute to a grid of criteria for judging the effectiveness of labwork. It will be used through two activities, evaluating a number of innovative teaching sequences, and surveying teachers' goals for labwork against what is really achieved in the six European countries.
(Dr. Séré's
contact information)
IUPAP - General Assemby Meets in Uppsala
Paul J. Black, Kings College London, UK;
ICPE Chairman
IUPAP held its 22nd General Assembly in Uppsala in September 1996. The Union has 45 member countries, with about 9 more applying to become members. Each country is represented by its national physics society. A general assembly is held every three years; 87 delegates attended the Uppsala meeting.
The general assembly elects an executive and the members for 20 IUPAP commissions. Each commission promotes international collaboration within a particular field of physics. ICPE - C 14 - is one of these. One of the changes decided in Uppsala was to give the commissions a stronger say in the work of IUPAP by requiring that the executive should include in its membership five vice-presidents elected from among the chairs of the commissions. The Assembly also asked the executive to set up a review of the structure and election to commissions in order to reduce overlap and enhance collaboration. Commission chairs will be called to a special meeting in the next few months to discuss these issues with the executive.
IUPAP is financed by subscriptions from the member countries. The executive receives applications from commissions for grants in support of the conferences that they sponsor-about 55% of the total expenditure is used for such support. Over the last three years, nine conferences sponsored by ICPE have been supported in this way, and two more have just been accepted for support in 1997. The IUPAP also gives ICPE a grant to support the cost of this newsletter.
The assembly agreed to set up a new commission, C20, on Computational Physics, to promote exchange and collaboration in an area where, through both development of numerical and symbolic models in theoretical work and through the control and data processing of experiments, computational methods are assuming increasing importance for physics. Another working group will continue to study the problems of communication amongst physicists: here there is both the pressure of the rapidly increasing numbers and costs of printed journals, and the prospect that electronic communication can replace paper means entirely and might be more closely controlled by the international physics community.
The work of all the commissions was reviewed during the assembly. Strong interest and support were expressed for the work of ICPE. Copies of our last newsletter were distributed at the meeting and it is clear that the other commissions would be willing to help with our work if new means of liaison can be established.
In his address as retiring president, Professor Yamaguchi
from Japan proposed that the Union should pay more attention to the work
of applied physicists. He outlined three other priorities: helping the
work of physicists in developing countries, moving away from science for
defence to science for development, and attracting more young people into
physics. In later discussion, these points received strong support, and
the executive will be studying ways in which the Union can help to promote
the public understanding of physics.
New Text Book: Physics For Life
UNESCO foundation course in physics education for non-physics majors
R. Kamel Wassef, Cairo University, Egypt
This is a text book for a two- or three-semester physics course for students who are not majoring in physics. These students need to know physics in context. The following principles were taken into consideration in designing this book:
· Physics is taught for life and not for school.
· Physics is taught to tell a story, not traditionally.
· Few formula derivations are given.
· Modern physics and new discoveries are included.
· Computer, video, & modern aids are to be used.
One of the main objectives in the book is to present a
modern view of physics. It is hoped that the study of physics in this way
will enrich the apprecaition and enjoyment of the physical world, and will
increase the students' personal resposibility as a citizen of the 21st
century.
For information contact the publisher at:
Dar Al Nashr for Egyptian Universities
16 Adly Street, PO Box 1347
Cairo 11511, Egypt
fax: 20-2-3912209
Or contact Dr. Wassef at
email: raafat@frcu.eun.eg
IUPAP SPONSORED:
Taller Iberoamericano de Ensenanza
de la Fisica Universitaria
20-24 January 1997
Havana, Cuba
The main field of the meeting will be university physics education, stressing:
· Automation of experiments and use of microcomputers in the laboratory
· Curricula design to retain 1st year students
· Physics teaching for non-physicists.
Contact:
Dr. Octavio Calzadilla-Amaya
Facultad de Fisica
Universidad de La Habana
10400 Ciudad de La Habana, Cuba
fax 537-33-3758
email: tibero@dialnet.cu
VI Inter-American Conference on Physics Education
30 June - 3 July 1997
Cordoba, Argentina
· New technologies in the classroom
· Updating the physics curriculum at all levels
· Incorporation of physics education into teacher preparation
· History & epistomology of physics education
Contact:
Dr. Alberto Maiztegui
Casilla De Correo 36
5000 - Cordoba, Argentina
fax: 54-51-229687
email: maiz@famaf.uncor.edu
Creativity in Physics Education
18 - 24 August 1997
Sopron, Hungary
· New Approaches in physics teaching
· Cultures of international science teaching
· Computer and multimedia in physics
· New technology and equipment in experiments
· Workshops on creative computer programming, experiments, & problem solving
Registration fee: US$250.
Contact:
Dr. George Marx
Dept of Atomic Physics, Eötvös University
Pushkin 5
Budapest H-1088, Hungary
fax: 36-1-2660206
email: marx@hercules.elte.hu
OTHER CONFERENCES OF INTEREST:
First European Conference on
Physics Teaching in Engineering
4- 6 June 1997
Copenhagen, Denmark
· What engineers & industry need from physics
· Teaching strategies
· Small/large groups
· Inclusion of modern physics
· Development of learning skills on physics
· Differentiation of core curriculum for different engineering branches
· Computer-aided teaching
Registration fee 800DKR
Contact:
Erik Oehlenschlaeger
PTEE 1997
Engineering College of Copenhagen
Lautrupvang 15
DK-2750 Ballerup, Denmark
fax: 45-44-97-22-20
email: eoe@iktmail.cph.ih.dk
The Third Australian Conference on Computers in University Physics Education (OzCUPE3)
2 - 4 April 1997
Brisbane, Australia
Conference theme, "A Diversity of Approaches":
· The use of computers in educational research,
· Teaching of computational physics,
· Computers in the laboratory, simulation, software.
Registration fee AU$290.
Contact:
J. Davies
PO Box 12230
Brisbane Elizabeth Street
QLD 4002, Australia
fax: 61-7-3864-1521
email: j.davies@qut.edu.au
First Conference of the European Science Education Research Association (ESERA)
2-6 September 1997
Rome, Italy
· Teacher education
· Experimental activities in science education
· The populariztion of science
· Educational methodology
· Teaching/learning processes in science education
Registration fee: US$150 for ESERA members
Contact:
Mrs. Gisella Pellegrini
Instituto di Psicologia del CNR, Roma
Viale Marx 15
00137 - Roma, Italy
fax: 39-6-824737
email: pellegri@kant.irmkant.rm.cnr.it
Trends in International Mathematics and Science Study (TIMSS)
With data on half a million students from 41 countries,
the Trends in International Mathematics and Science Study (TIMSS) is the largest
and most comprehensive international study of schools and students ever.
The report, Pursuing Excellence, is a synthesis of initial findings from
TIMSS on the U.S. eighth grade mathematics and science education, providing
a comparative picture of education in the United States and the world that
sheds new light on education in the U.S. through the prism of other countries.
Also available for study are findings and sample lessons from the TIMSS
Videotape Classroom report of 8th grade mathematics with Germany, Japan,
and the U.S.
International Commission on Physics Education
Information on ICPE including history, current projects,
and the latest newletters (this one will be there as well). Also links
to physics education journals, research groups, newslists, & organizations.
Collections and Indexes
Cornell Theory Center Math & Science Gateway
http://www.tc.cornell.edu:80/Edu/MathSci Gateway/
Index of sites in many science disciplines.
Frank Potter's Science Gems
Huge list of science resources on the web. Problems,
museums, research sites, classroom techniques, etc. Divided by subject
and by grade-level.
World Internet Directory, Math and Science Education
http://www.tradenet.it/links/arsocu/science_education.html
Several dozen links to science and math education sites
in no particular order.
The Internet Pilot to Physics
A wide-ranging resource. Includes a listing of physics
institutions by country, a job listing, a physics e-zine (a magazine published
on the web), a searchable database of European papers, chat rooms, etc.
Galaxy
http://www.einet.net/galaxy/Science/Physics.html
Very large index of physics institutionsand organizations. This page is part of a larger index. Browse up to "science" to get an index of resources for other sciences or down through various subheadings.
Explorer
Index of downloadable software for teaching math and science
skills. Mostly for primary and secondary school. Includes a huge list of
links to interesting science-related and educational sites.
Science in the Classroom
Contemporary Physics Education Program (CPEP)
Includes interactive, detailed tours of the inner workings
of the atom and of fusion and plasma physics.
Shodor Education Foundation's Master Tools
Interactive simulation environments that include programs
to build your own universe, explore fractals, explore surface movement
of electrons, and model a pendulum.
Science Fiction Manned Spacecraft Systems
http://tommy.jsc.nasa.gov/~woodfill/SPACEED/SEHHTML/scifi.html
This site encourages students to analyze spacecraft and
space activities from science fiction stories and art by comparing them
with the reality of physics.
Live from the Hubble Space Telescope
http://quest.arc.nasa.gov/hst/tg/intro.html
How teachers can use images from the Hubble Space Telescope
in their classrooms.
Center of Excellence for Science & Mathematics Education
http://www.utm.edu/~cesme/index.htm
Contains a collection of activities, a calendar of events,
and list of additional resources. Mostly for K-12.
The Franklin Institute
The Franklin Institute is a hands-on museum of science
and industry in Philadelphia, Pennsylvania. This site is aimed mostly at
younger students, but has some interesting experiment and demonstration
ideas in the science fair area. (Click on "on line exhibits",
then "spotlights", then "science fair".)
And Finally
The Science Joke Index
http://www.xs4all.nl/~jcdverha/scijokes/
Jokes about the major branches of science, anecdotes about
famous scientists/mathematicians, "A physicist, an engineer, and a
mathematician…" jokes, sources for more humor.
European Physical Society Creates Forum on Education
Gunnar Tibell, EPS Forum Chairman
The European Physical Society (EPS) decided in 1994 to set up a Forum on Education as part of its Interdivisional Group on Education. The aim of the Forum was to encourage the interest for school education in physics among the national physical societies belonging to EPS. Two other parts of this interdivisional group aim at student mobility and university physics education, respectively. Already at its start the Forum was asked to send a representative to a jury set up to choose a winner in a physics textbook contest, initiated by the Italian Amaldi Foundation.
Somewhat later, an enquiry was made among the 37 physical societies about their concern for the questions at the centre of interest for the Forum. The results showed, as expected, a great variety of involvement in pre-college physics education. From the answers it was clear that in some countries the societies were very active in their contacts with schools. Among those, a Forum Board was set up; it now consists of ten members from nine different countries.
The Forum made its first "public" appearance at the EPS meeting, Trends in Physics, held in Sevilla in September, 1996. In a session devoted to education, several talks were given on relevant topics. We also had an invited speaker from the APS Forum on Education. It is of course important for our Forum to keep in touch with other organizations having the same aims. One such body is the Commission on Education of the International Union on Pure and Applied Physics (IUPAP), another one is GIREP.
Next the Forum will undertake a survey of European physics
curricula and try and arrange teacher's exchange programs in certain European
countries. Also, contacts with other similar organizations will be initiated
by different means. A more extensive report on the aims of the Forum can
be found in Europhysics News, Volume 27, p. 75 (March/April 1996).
| I am tired of all this thing called science here [referring to the
Smithsonian Institution]¼. We have spent
millions in that sort of thing for the last few years, and it is time it
should be stopped.
-US Senator Simon Cameron (1901) |
International Commission on Physics Education
IUPAP Commission 14
Chairman
Paul J. Black
Centre for Educational Studies
King's College London
Cornwell House Annex, Waterloo Road
London SE1 8WA, UK
fax: 44-171-872-3182
email: Paul.Black@kcl.ac.uk
Vice-Chairman
S. S. Krotov
Physical Department
Moscow State University
64A Leninsky Prospect
Moscow 117 296, Russia
Phone: +7-095-930-3632
bquantum@sovam.com
fax: 7-095-938-2140
Secretary
Anna M. P. de Carvalho
Faculdade de Educação
Universidade de São Paulo
Av. da Universidade 308
Cidade Universitária
05508-900 Paulo-SP, Brazil
fax: 55-11-818-3149
Members
Uri Ganiel
Department of Science Teaching
Weizmann Institute of Science
PO Box 26, Rehovot 76100, Israel
fax: 972-8-9344-115
email: ntganiel@weizmann.weizmann.as.il
Max Kesselberg
Fysikum, Stockholm University
Box 6730
S-113 85 Stockholm, Sweden
fax: 46-8-347-817
email: kesselberg@physto.se
Piet Lijnse
Department of Physics
Utrecht University
PO Box 80.008
NL-3508 TA Utrecht, Netherlands
fax: 31030-2517-629
email: p.l.lijnse@fys.ruu.nl
Wei-Yin Luo
College of Advanced Continuing Education
Zhongshan University
Guanzhou 104/57a
S.W. District
Guangzhou 510275, PR China
fax: 86-20-418-9173
N. Mukunda
Centre for Theoretical Studies
Indian Institute of Science
Bangalore 560 012, India
fax: 91-80-334-1683
E. F. Redish
Department of Physics
University of Maryland
College Park, MD 20742, USA
fax: 1-301-405-6114
email: redish@quark.umd.edu
Tae Ryu
Department of Physics
Sophia University
7-1 Kioicho, Chiyoda-ku
Tokyo 102, Japan
fax: 81-3-3238-3341
J. Sahm
Technische Universität Berlin
Fachbereich Physik
Hardenbergstr. 36
D-110623 Berlin, Germany
fax: 49-30-314-23057
M. G. Séré
DidaSCO
Université Paris XI. Bat 333
F-91405 Orsay Cedex, France
fax : 01 64 46 33 25
email: sere@idf.ext.jussieu.fr
J. R. Seretlo
University of Fort Hare
Faculty of Science
PO Box 21
Fort Hare 5701, South Africa
fax: 27-404-31-669
Associate Members
E. Lillethun
Department of Physics
University of Bergen
Alleg. 55
N-5007 Bergen, Norway
fax: 47-55-318-334
M. A. Moreira
Instituto de Fisica - UFRGS
Caixa Postal 15051
91500 Porte Alegre, RS, Brazil
fax: 55-51-336-1762
S. W. Raither
UNESCO Div. of Scientific Research &
Higher Education
1 rue Miollis
F-75015 Paris, France
fax: 33-1-4567-2639
| From the time computers came I was afraid of the day my students would
know more about programming than I ever will. At the beginning I had a
big advantage. I came fresh from a summer workshop on Logo and the students
were just beginning.
But I knew that each year the children would know more because they would have had experience in previous grades, and because each year more of them would have computers at home. I struggled to avoid facing the fact that I could not keep up my stance of knowing more than they did. I was afraid that giving up this stance would undermine my authority as a teacher. Eventually I broke down and said "I don't understand your problem. Go discuss it with some of the others in the class who might be able to help." Working together, the kids could figure out a solution. Now the amazing thing is that what I was afraid of turned out to be a liberation. I realized that my bluff was called for more than computers. I felt I could no longer pretend to know everything in other subjects as well. My class has become much more of a collaborative community where we are all learning. -Seymour Papert from "The Connected Family: Bridging the Digital Generation Gap" (Longstreet, 1996) |
The International Newsletter on Physics Educaiton
is a publication of the International Commission on Physics Education and
is produced twice a year. For comments, questions, or to be added to or
deleted from the mailing list, please contact one of the editors. Article
submissions and announcements are always welcome.
Editor: Dr. Edward F. Redish
Associate Editor: Daniel Campbell
University of Maryland
Department of Physics
College Park, MD 20742
fax: 1-301-314-9525
email: redish@quark.umd.edu
or: dcampbel@delphi.umd.edu
| IUPAP | ICPE | Newsletters |
|---|---|---|

|
 |
 |